Yes, I know the title is slang for “hang by the neck until dead”. Pressing on…
The Elastic Catenary Problem
I wanted to examine a variation on the catenary problem, called the elastic catenary problem. Now the hanging rope, chain or cable can stretch under tension. This is a bit more realistic when using catenaries for e.g. bridge supports - even steel cables are a bit elastic, and the elasticity must be taken into account if you want your bridge to not fall down. The elasticity introduces some differences from the normal non-elastic catenary problem:
- The rope can now store potential energy by virtue of it being stretchable. The rope can be modeled as a spring that obeys Hooke’s Law with a spring constant \(k\) and an unstretched length of \(L_{0}\). Thus there will be an additional term in the Lagrangian for potential energy, though there is still no kinetic energy term.
- Because the length of the rope is no longer constant, we don’t have to introduce a constraint that keeps it constant, so we don’t have to bother with Lagrange multipliers in the solution.
- Also because the rope can stretch, and the stretch is always along its length, the amount of potential energy it stores is not constant - the rope stretches more near the supports (and stores more potential energy) than it does near the bottom of the catenary.
- Likewise, the mass density along the rope is not constant - the density is greater where the rope is not stretched so much.
Solving this problem with the Euler-Lagrange equations is quite messy, so as in the previous posts in this series, I used “Vibe Physics” to get a solution to the elastic catenary problem with AI, presented in the post Vibe Physics: Elastic Catenary Solution. Those really interested in what a vibe physics solution looks like can read that post.
The reason I went through all that physics was to get some math out of it, such that I could incorporate it into a coding project. I mentioned in The Earth Moved, And So Did the Code (to the Web!) that I have some interest in how a straightforward physical simulation can ‘solve’ complicated differential equations just by settling to a steady state. I realized that the code that simulated the masses-on-springs system in that project could also be used to solve the elastic catenary problem, which vibe physics told us corresponds to a nasty non-linear differential equation of the form
\[y'' = \frac{\sqrt{1 + (y')^2}}{a(1 + \beta\sqrt{1 + (y')^2})}\]Vibe physics also told us though that the solution should be pretty similar to the non-elastic catenary discussed in Vibe Physics, especially when the \(k\) values are large, which corresponds to stiff springs.
I built a web app to demonstrate this and compare the elastic and non-elastic catenary cases.
The Elastic Catenary App
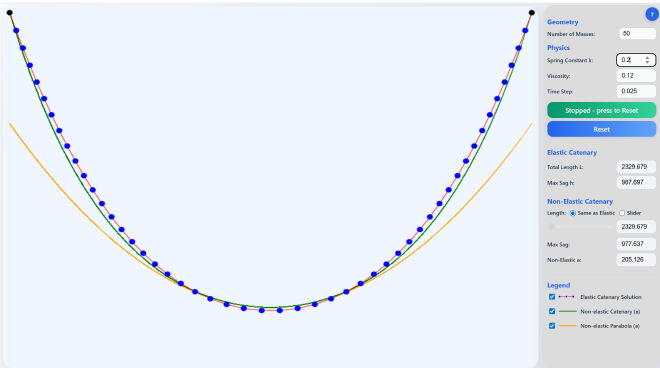
The Elastic Catenary Web App
Starting with the code from The Earth Moved…, I constructed a web app to illustrate and check the solution to the elastic catenary problem, you can run it here. As you may notice if you’ve run the previous web app referenced above, this is basically a single line of masses on springs instead of a 2D matrix of masses on springs. This single line of masses on springs solves the elastic catenary differential equation. The app also calculates and plots the solution to the non-elastic catenary problem, which recall from Vibe Physics has the equation
\[y = a\,\cosh\!\left(\frac{x - x_0}{a}\right) + y_0\]The ‘point of contact’ between the elastic and non-elastic catenary solutions is the length \(L\) of the rope. In the elastic catenary, this length changes as the app runs because the rope can stretch. In the non-elastic catenary, the length is constant. So when plotting the non-elastic catenary, we need a value for \(L\). Where we get this \(L\) from is determined by the Length radio buttons in the app: either from the current length of the elastic rope (calculated by adding up all the spring lengths), or from the position of the slider. The slider can be used to set the length of the non-elastic catenary to any value, just for fun. Whichever way the length \(L\) is obtained, it is used to numerically solve the transcendental equation
\[L = 2a\sinh\!\left(\frac{x_0}{a}\right)\]for the catenary parameter \(a\), using the bisection method mentioned in the vibe physics catenary solution post. \(x_0\) is half the distance between the rope supports, which is arbitrarily set to 1000 in the app. Knowing the value of \(a\) allows the non-elastic catenary to be plotted as the green line.
Just for reference, the parabola that approximates the non-elastic catenary (as discussed in the Vibe Physics post) is also plotted as the orange line, which you can turn off in the Legend section.
The app itself was not quite vibe coded, but fairly heavily AI-assisted I’d say.
You can press the blue help button in the app for some info on the app details.
Playing with the App
When the app starts, the springs and masses are completely unstretched, so the rope falls then bounces a bit until it reaches equilibrium state. By default, the “Same as Elastic” radio button is ticked, so the length \(L\) for non-elastic catenary shape is the current Total Length \(L\) of the elastic rope.
Note that as the rope is falling into its equilibrium position, the springs near the supports start stretching first, and the shape initially formed by the rope is not very catenary-like. The initial stretching at the sides makes the calculated length of the elastic rope larger, and when this larger \(L\) is used to calculate the non-elastic catenary, it causes the green line to sag more quickly than does the rope. But as the tension becomes more evenly distributed in the rope, the calculated length becomes closer to that for an actual catenary, and the rope catches up to and matches the green line.
The most important parameter is the Spring Constant \(k\). When it is at its default value of 10, which corresponds to stiff springs, you can see that the green line is right on top of the rope. This corresponds to the statement that the solution for the elastic catenary approaches the solution for the non-elastic catenary as the rope becomes more non-elastic.
However, as you make the Spring Constant \(k\) smaller, say to a value of 1, you can start to see differences between the elastic rope solution and the non-elastic catenary green line. As the rope becomes more elastic (smaller \(k\)), the shape that it makes sags more in the middle and thins out at the sides. So the rope is below the green line in the middle and above the green line on the sides. Correspondingly, the displayed Max Sag value is slightly larger for the elastic catenary than for the non-elastic catenary. The screenshot above shows a \(k\) value of 0.2, which is a pretty stretchy rope.
Summary
OK, that was a lot of work in both physics and in code just to see some tiny differences between red and green lines. All that time and effort could not be justified if the goal was to produce a useful app. Yet, this project entertained me, helped me brush up on some physics, and taught me a bit more about TypeScript and React. Projects undertaken just for entertainment and educational value don’t have to meet any business goals.
