Vibe Physics

I had occasion recently to go back and review some physics in classical mechanics. Along the way, I “discovered” (in the personal sense, not in the global sense) a technique called “Vibe Physics”, in analogy with Vibe Coding. It turns out that you can solve physics problems with AI in much the same fashion that you can have AI write code for you - by just prompting AI over and over to produce the solution, accepting what it produced at each step, and after each step telling it what is wrong or what you want changed. Repeat this until either you are happy with the physics (or code), or it becomes clear that the procedure won’t converge. The fact that vibe physics worked for me was very interesting to me, so I’m kicking off a series of posts with it.

Classical Catenaries

As a bit of an offshoot from a for-fun software project I’m doing (stay tuned), I wanted to analyze the shape that a hanging chain or rope makes, which is called a catenary.

Figuring out the shape of a catenary is a classic problem in classical mechanics, and one that is usually treated early on in classical mechanics textbooks, e.g. on page 42 out of 672 in Goldstein’s Classical Mechanics. In these treatments the chain or rope is assumed to be perfectly flexible and has a total length that does not stretch.

This problem can be solved with the Euler-Lagrange equations (See Lazy Physics: Least Action).¹ The problem is easy in the sense that the Lagrangian only has potential energy, no kinetic energy. It does require a shift in thinking because we are looking for a solution that is the shape of the rope or chain \(y(x)\) that is a function of \(x\), not \(t.\) The derivatives in the Euler-Lagrange equations are with respect to \(x\), not \(t.\) And, the constraint on the problem that the length of the chain or rope remains constant adds a mathematical wrinkle that must be ironed out with Lagrange multipliers, which adds complexity. Not to mention that there are some tedious steps in the derivation itself that makes the problem a bit difficult.

I was going to present the solution to the catenary problem in this post, but I got a bit bogged down in the math. So I asked AI for help.

Feel the Vibe

You can ask ChatGPT to:

Show using the Euler-Lagrange equations to solve the catenary problem

and it shows you the solution, step-by-step, including some fairly gnarly derivatives and integrals that are needed on the way to the solution.

Initially I was very impressed with the solution ChatGPT produced, but as I looked at the steps more closely, I realized that it made mistakes in several places, although it still arrived at the right answer at the end. I can relate to this: I remember in college that my fellow physics students and I developed a technique for getting past some nasty homework problems that we called “The Ol’ Lose ‘Em in the Page Turn”, where we started from the beginning with some steps towards the solution, and then worked backwards from the answer (that was often given when the problem was a ‘Show that …’ style problem), and arranged for the ’then a miracle happens here’ step in the middle of the solution to be right on a page turn. The first step on the new page didn’t follow at all from the last step on the previous page, yet unless the homework grader looked very carefully, flipping back and forth between the pages, they wouldn’t notice because the steps seemingly arrived at the correct answer. This scam sometimes worked with the grad students who were grading the physics homework.

Except, AI didn’t bother to hide the faulty steps on a page boundary. Anyway, the lesson is: don’t trust what AI produces, always verify. Same with physics students I guess.

For the catenary problem, I ended up starting over and asking a different AI tool and model (claude 4 sonnet in Warp) for the solution. AI again produced a solution that had several errors, but obtained the right answer at the end regardless. When I pointed out the errors in the steps through additional prompts, and asked it to explain certain steps more clearly, it fixed the errors, and moved towards the correct solution. After many prompts and iterations, it eventually converged to a solution that I was happy with. It seemed correct at every step. I then went further and asked AI to turn the solution into a blog post, complete with math equations and even a diagram to go along with the problem. AI also generated the top-level image associated with the post itself. The end result is the next post in this series, Vibe Physics: Catenary Solution. There was no additional hand editing done to this post by a human - the post content was created strictly by prompting and re-prompting AI. Note that I gave dual authorship for that post to Artificial Intelligence and myself, as we both put some work into it - my part was to act like a physics homework grader and point out where it had made mistakes or didn’t show it’s work sufficiently.

While the catenary problem is generally considered to be pretty easy, I always thought it was more complicated than it was given credit for. If you read through the AI solution, note all the physics and mathematics that AI (or a physics student) must understand and be handy with to get to the solution. A partial list includes:

• expressing the gravitational potential energy in a chain or rope
• calculus of variations and/or using Euler-Lagrange equation
• how to incorporate constraints with Lagrange multipliers
• partial derivatives
• significant dexterity with taking ordinary derivatives (chain rule, product and quotient rules)
• solving ordinary differential equations via integration, including knowing that one of the integrals encountered in the problem is an inverse hyperbolic cosine - that doesn’t come up every day…
• significant algebra, including simplifying equations and integrals by making variable substitutions
• knowledge of logarithms and exponentials
• keeping track of integration constants, setting them so that initial conditions are satisfied
• hyperbolic trig identities

This is a fairly impressive list in my opinion.

Interesting side note: when I asked AI to produce the images to go along with the catenary post, I thought it might use agentic AI to task some separate specialized image generator AI with producing the images. Instead it generated standalone Python programs that when executed produced the SVG images!

Catenary Takeaways

From Vibe Physics: Catenary Solution, the differential equation to solve to get the catenary solution is

\[y'' = \frac{1 + (y')^2}{y - a}\]

Solving this differential equation gives the equation for the catenary curve that can be written as

\[y = a\,\cosh\!\left(\frac{x - x_0}{a}\right) + y_0\]

where cosh() is the hyperbolic cosine function, which is shorthand for

\[\cosh(x) = \frac{e^{x} + e^{-x}}{2}\]

and \(a\), \(x_0\), and \(y_0\) are constants. The \(x_0\) and \(y_0\) just determine the overall position of the catenary curve, but the \(a\) constant is more interesting and must usually be solved for numerically from the transcendental equation

\[L = 2a\sinh\!\left(\frac{x_0}{a}\right)\]

where \(L\) is the length of the rope, and \(x_0\) is the distance from the center to the supports for the rope.

It is interesting to note that, while the solution looks a lot like a parabola, it is not quite a parabola, as is depicted by this (ChatGPT-generated) graph:

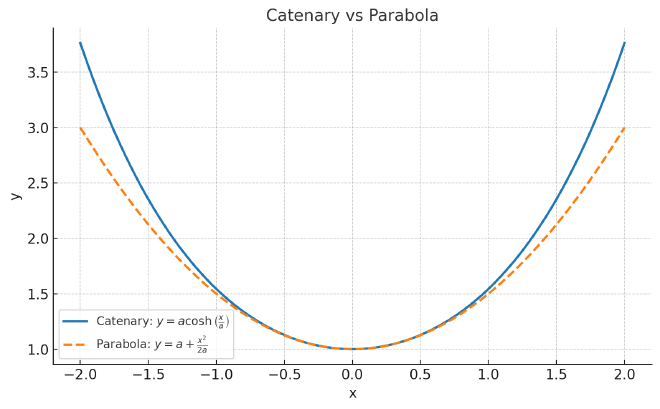
The equation of the parabola that most closely matches the catenary is

\[y = \frac{x^2}{2a} + a\]

Summary

This is going somewhere I promise, stay tuned for the next articles in the series…

I have seen claims that Vibe Physics can help career physicists make meaningful advances in physics. I don’t think this is possible with ‘off-the-shelf’ popular LLMs, just because their training sets haven’t included enough recent, cutting-edge physics. Helping with college-level homework problems is one thing, contributing to publishable physics is another. It may be possible to extend and specialize a general-purpose LLM by fine tuning it with many research papers on a particular area of physics to make the customized LLM knowledgeable enough to be helpful in producing new results in that area. But fine tuning can be expensive and is hit or miss.

But I wonder if Vibe Physics is what college physics has now become. Maybe the essential skill that you need to learn as a physics student is the ability to recognize errors in a solution produced by AI, and the know-how to correct those errors through additional AI prompts. I suspect that there is no way that homework graders can tell whether a student used AI instead of solving the problem the old-school way.

Professors, researchers and homework graders have to be on the lookout for the modern AI-generated equivalent of “The Ol’ Lose ‘Em in the Page Turn” con.